Vou te confessar uma coisa: De todos os assuntos que ensino na matemática, a geometria é a mais bonita. E dentre os assuntos da geometria, o cilindro é a figura mais legal. Então vem comigo descobrir área e volume do cilindro e conhecer tudo o que você precisa saber sobre essa figura mágica da geometria espacial. Bora lá?
Clique aqui para ser aprovado no próximo concurso que prestar
O Que É o Cilindro?
Cilindro é um sólido geométrico que é estudado na geometria espacial. Mas por que isso? Essa figura é estudada na geometria espacial porque é dotado de volume.
Para ficar claro na sua cabeça, o melhor exemplo de cilindro é aquele papelão que sobra quando o papel higiênico acaba.
Outro exemplo é a latinha de refrigerante. Desconsiderando pequenas alterações no formato próximo às bases, a latinha de alumínio é um cilindro também.
Como um Cilindro é Formado?
O cilindro é formado por duas bases circulares iguais ligadas por uma área lateral.
O estudo dessa figura é muito comum em concursos públicos ou outras provas por aí. E existem alguns conceitos importantes que quero que você saiba para matar todas as questões desse assunto daqui em diante.
Elementos do Cilindro
Como eu escrevi acima, o cilindro é dotado de dois círculos como bases, e todo círculo tem um raio. Todo cilindro também possui uma altura, assim como a latinha de refri ou o rolo de papel higiênico têm suas alturas.
Além disso se você planificar um cilindro, ele se torna um retângulo ou quadrado como área lateral. Imagina que você pega um rolo de papel higiênico e corta de fora a fora. Aí você vai abrir esse cilindro, tornando-se um retângulo. Disso nós podemos ter os principais elementos do cilindro:
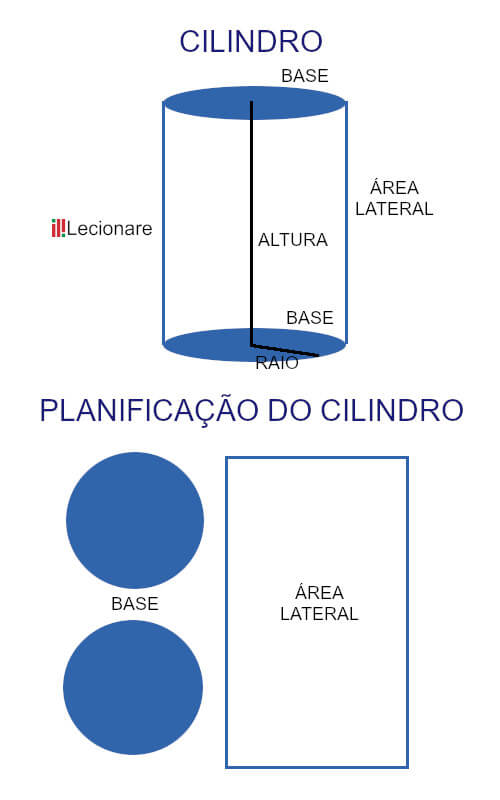
- Base: duas bases circulares idênticas (superior e inferior)
- Raio: todo círculo tem raio que é a distância entre o centro até a extremidade
- Altura: é o comprimento do cilindro, ou a distância entre as bases
- Área lateral: Com a planificação completa da figura, a área lateral se torna um retângulo (ou quadrado).
Áreas do Cilindro
O cilindro possui basicamente 3 três áreas diferentes: Áreas das bases (que são iguais), área lateral (aquele quadrado ou retângulo do cilindro planificado e área total (soma das bases mais lateral).
Agora eu quero esmiuçar cada uma delas para você entender de vez. Vamos lá?
Área da Base do Cilindro
Como escrito acima, as bases de um cilindro é um círculo. Aí vamos voltar para conceitos básicos da geometria plana. Você lembra como calcula a área de um círculo? Área do círuclo é igual a constante Pi x raio elevado ao quadrado.
“Pierre Quadrado”. Fica um nome meio francês, não é mesmo? Foi assim que eu guardei essa fórmula. Área do círculo é um francês chamado Pierre Quadrado. =)
Área da Base = Área do círculo = π(Pi) x Raio²
Vamos a um exemplo qualquer. Quanto é a área de uma base do círculo de raio 5? Vamos aos cálculos.
Área da Base = π x Raio²
Quanto ninguém fala o valor exato de Pi, considere aproximadamente 3,14, ok?
Área da Base = 3,14 x 5²
Área da Base = 3,14 x 25
Área da Base = 78,5
Área Lateral do Cilindro
Na figura acima você percebeu que quando “cortamos de fora a fora” o papelão do papel higiênico, ele se torna um quadrado ou retângulo, dependendo do caso. Então a área lateral de um cilindro é justamente a área dessa nova figura em que a base é igual a circunferência da base e a altura é a altura do próprio cilindro:
Área Lateral = base x altura do cilindro
Agora você lembra quanto é a circunferência de um círculo? Circunferência é igual a 2 x Pi x Raio:
Área Lateral = 2πR x altura do cilindro
Vamos ao exemplo anterior. Quanto é a área lateral de um cilindro com raio de base igual a 5 e altura 10?
Área Lateral = 2πR x altura do cilindro
Área Lateral = 2 x 3,14 x 5 x 10
Área Lateral = 31,4 x 10
Área Lateral = 314
Área Total do Cilindro
Área total é a soma de todas as áreas já calculadas do cilindro. Então um sólido cilíndrico tem duas bases iguais (inferior e superior) e área lateral.
Vamos voltar ao mesmo exemplo: Qual é a área total de um cilindro com raio na base igual a 5 e altura 10?
Área total = 2 x Área da Base + Área Lateral
Área total = 2 x 78,5 + 314
Área total = 157 + 314
Área total = 471
Volume de Cilindro
O volume do cilindro é calculado pela área da base multiplicada pela altura. Essa forma de calcular volume é, inclusive, válido para qualquer sólido regular.
Como a base do cilindro é um círculo, vamos calcular a área do círculo e multiplicar pela sua altura:
Volume do Cilindro = Área da Base x altura
Vamos a um exemplo novo. Qual é o volume de um cilindro de raio 6 na base e altura 8?
Volume do Cilindro = Área da Base x altura
Volume do Cilindro = Área do Círculo x altura
Volume do Cilindro = π x Raio² x altura
Volume do Cilindro = 3,14 x 6² x 8
Volume do Cilindro = 3,14 x 36 x 8
Volume do Cilindro = 3,14 x 288
Volume do Cilindro = 904,32 unidades cúbicas
Questão Desafio Nas Redes Sociais Lecionare
Agora com toda essa teoria fresquinha na sua cabeça, você será capaz de decifrar o desafio que postei nas redes sociais Lecionare.
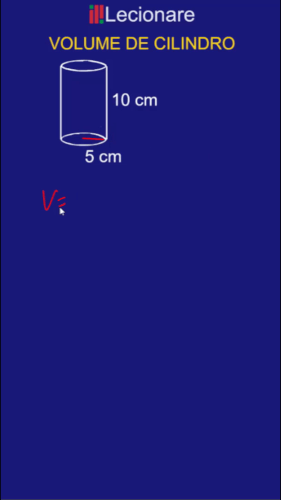
Qual é o volume de um cilindro de raio 5 cm e altura 10 cm?
Vamos aos cálculos: Qual é o volume do cilindro? Área da base multiplicada pela altura:
Volume Cilindro = Área Base x altura
Volume Cilindro = π x Raio² x altura
Volume Cilindro = π x 5² x 10
Volume Cilindro = 3,14 x 25 x 10
Volume Cilindro = 3,14 x 250
Volume Cilindro = 785 cm³
Ufa! Vencemos mais uma. É de pequenas conquistas que uma aprovação é construída. E pode anotar na sua conta que você está no caminho certo. E o assunto e fórmulas principais sobre o cilindro você já viu. Agora é partir para os exercícios.
Gostou do que leu aqui sobre o cilindro na matemática? Então eu quero te fazer um convite.
Quero te convidar a se inscrever no canal do Lecionare no Youtube porque lá são postados muitos conteúdos que vão te ajudar a ser aprovado. Tudo gratuito. Tem correções de provas, técnicas de estudo e de inteligência emocional, resoluções de provas, novos concursos e muito mais.
E tem também o perfil do Instagram com desafios, informações e muito mais. Segue lá.
Eu te desejo bons estudos, boa sorte e até a próxima.
Tamo Junto Até a Sua Aprovação
